딥러닝(Deep Learning), 인공신경망, 퍼셉트론
딥러닝(Deep Learning)과 머신러닝(Machine Learning)
딥러닝과 머신러닝은 컴퓨터에게 스스로 학습을 시키고 마치 사람처럼 스스로 의사결정을 할 수 있게 한다. 예를 들어 사진을 보고 무엇인지 분류하는 분류 모델의 경우 학습에 필요한 이미지와 해당 이미지에 대한 정답 데이터를 모델에게 제공하여 분류할 수 있도록 만든다. 이것을 지도학습이라고 한다. 여기서 딥러닝과 머신러닝의 차이가 있다. 딥러닝은 데이터에서 특징값(Feature)을 스스로 찾아내는 반면, 머신러닝은 이 특징값을 직접 추출하여 해당 특징을 통해 학습을 한다. 그래서 머신러닝에서는 모델에서 추출한 특징값이 얼마나 데이터를 잘 대표하는가에 따라 모델의 정확도가 크게 바뀐다.
특징값을 스스로 찾아내는 딥러닝은 학습 과정에서 목표를 잘 달성할 수 있는 특성인자를 스스로 찾기 때문에 특성인자를 직접 뽑아줘야 하는 머신러닝에 비해 활용하려는 시도가 많이 늘어나고 있다.

인공 신경망(Neural networks)
인공 신경망은 생물학의 신경망에서 영감을 얻은 수학적 모델이다. 딥러닝은 이러한 인공 신경망을 이용한 학습을 한다. 딥러닝에서 인공신경망은 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)로 이루어진다. 각 층에는 뉴런들이 배치되어 있고 해당 뉴런들은 가중치를 통해 연결되어 있다. 이렇게 연결되어있는 뉴런들은 활성화 함수를 통해 데이터를 넘길지 말지 결정한다. 여기서 활성화 함수는 뉴런에 일정량 이상의 자극을 받을 때 해당 뉴런을 활성화 시키는 함수이다. 이러한 뉴런을 기반으로한 알고리즘으로 퍼셉트론(Perceptron)이 있다.
퍼셉트론은 뉴런과 마찬가지로 다수의 신호를 입력받고 하나의 신호로 출력할 수 있다. 퍼셉트론의 신호는 흐른다/흐르지 않는다. 즉 1과 0으로 표현할 수 있다. 일반적으로 신호가 흐를 때 1로 표현하며 흐리지 않을 때 0으로 표현한다. 또한, 퍼셉트론도 뉴런가 마찬가지로 일정 크기 이상의 자극을 받아야 신호를 출력한다. 다음 이미지는 퍼셉트론을 표현할 때 자주 표현되는 이미지이다.
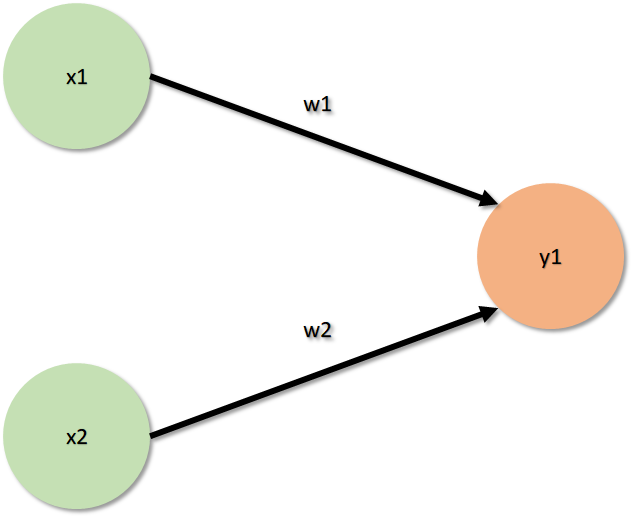
위 그림에서 x1과 x2는 입력을 뜻하고 w1, w2는 가중치, y1는 출력을 의미한다. 다음 이미지에서 y1의 출력값은 x1w1+x2w2의 값으로 정해지며 해당 값이 일정 수치 이상이면 y1은 1을 출력하고 수치 미만이라면 0을 출락할 것이다.
이러한 퍼셉트론이 여러 개 여러 층이 쌓이면 다층 퍼셉트론이 된다. 이 다층 퍼셉트론이 인공 신경망이다. 다층 퍼셉트론의 형태는 다음 이미지와 같다.

기존의 퍼셉트론에서 층이 늘어난 형태로 단일 퍼셉트론은 AND, OR, NAND 연산까지 할 수 있었다면 다층 퍼셉트론은 XOR 연산까지 할 수 있다.
단층 퍼셉트론 사용 시 활성화 함수가 선형으로 이루어지지만 다층 퍼셉트론을 사용하면 활성화 함수가 비선형으로 이루어진다. 즉, 단층 퍼셉트론은 데이터의 값이 기준선을 넘어가야 다음 뉴런이 활성화가 되는데 이 기준선의 형태가 직선의 형태이고 다층 퍼셉트론은 기준선의 형태가 곡선의 형태로 만들 수 있다. 그래프로 표현하면 다음과 같다.

다층 퍼셉트론을 이용하면 복잡한 데이터에 대해 좀더 정확한 구분을 할 수 있다.
이러한 인공 신경망의 학습에서 중요한 것은 출력층에서 계산된 출력과 실제 출력의 값 차이를 최소화시키는 가중치를 찾는데 있다. 여기서 가중치는 위의 그래프에서 기준선을 의미한다. 기준선을 잘 설정할 수록 모델은 더욱 정확한 예측을 할 것이다. 딥러닝에서 문제를 해결할 최적의 가중치를 찾기 위해 목적 함수(Object function or loss function)를 정의한다. 목적 함수가 정의되면 가중치의 변화에 따른 오차의 변화를 계산할 수 있기 때문에 오차와 가중치의 관계를 연쇄법칙(Chain rule)을 이용한 편미분으로 구할 수 있게 된다. 일반적으로 stochastic gradient descent를 통해서 가중치를 반복적으로 갱신한다.
가중치 갱신은 출력층에서 부터 입력층으로 역방향으로 갱신이 진행된다. 이것을 오차역전파(Backpropagation)라고 한다. 오차역전파의 과정은 다음과 같다.
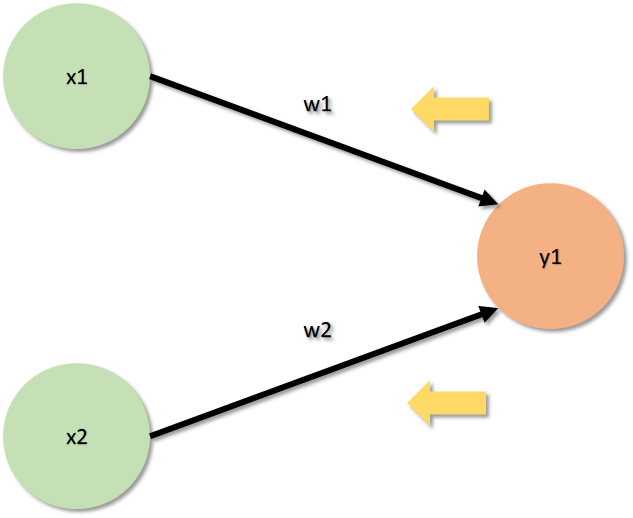
- 다음 그림의 x1, x2, y1은 이전에 주어진 값이다.
- 임의의 w1, w2를 설정한 뒤 y1을 계산한다.
- 새로 계산한 y1과 기존의 y1의 차이를 비교한다.
- 경사하강법을 이용하여 오차가 작아지는 방향으로 w1, w2를 수정한다.
- 오차가 더 이상 줄어들지 않을 때까지 위의 과정을 반복한다.
인공 신경망을 이용하기 위해서 사용자는 모델 구조와 데이터만 준비하면 된다. 여기서 사용자는 데이터를 학습에 사용될 수 있도록 일관된 포멧으로 맞춰주고 모델을 구조화한다. 그러면 모델이 학습하는 동안 데이터에서 특징들을 추출하며 학습을 이어간다. 정확도를 늘리기 위해 사용자는 모델 구조에 신경쓰고 알맞은 알고리즘을 적용시켜준다. 딥러닝에서는 입력, 은닉, 출력층이 있다고 했다. 특징을 추출하고 학습을 하는 주요 과정은 은닉층에서 이루어진다. 이 은닉층에 갯수를 얼마나 늘리고 각 층마다 어떤 활성화 함수를 사용하며 뉴런들을 어떻게 조작할지 튜닝을 하므로써 모델의 정확도가 늘어날 수 있다.
딥러닝은 여러 문제를 해결하기 위해서 다양한 구조의 알고리즘이 개발되었는데 그 중 대표적인 것이 합성곱 신경망(Convolutional neural networks)와 순환 신경망(Recurrent neural networks)이다. 이 두 가지 신경망은 각각 이미지와 자연어 처리에 특화된 신경망이다. 오토인코더(Autoencoder)도 복잡한 공학 문제를 해결하기 위해 개발되었다. 이전에 포스팅안 RNN, CNN이 있기 때문에 이 글에서는 오토인코더에 대해서 다루겠다.
오토인코더(Autoencoder)
오토인코더는 복잡한 공학문제를 해결하기 위해 사용된다. 대부분의 공학 문제는 그 문제의 이면에 존재하는 원리를 파악하면 쉽게 풀린다. 이 점을 이용하여 복잡한 데이터를 압축하여 간단히 표현하려는 노력이 이어지고 있다. 예로 Singular Value Decomposition(SVD) 또는 Principal Component Analysis(PCA)가 있다. SVD는 특이값 분해로 임의의 차원에서 행렬 A를 분해하여 표현하는 방법 중 하나이다. PCA는 주성분 분석으로 주성분 분석은 여러 클래스에서 평균을 구할 때 공정한 평균을 구하기 위해 각 클래스마다 가중치를 정하고 해당 가중치를 고려하여 평균을 구하는 것이다. 여기서 평균은 클래스들 사이의 값의 기준선을 의미한다.
이러한 오토인코더는 은닉 상태를 추론하여 문제를 풀어가는 알고리즘이다. 즉, 정답이 정해지지 않은 것에 대한 학습을 하고 그 답을 추측하는 모델이라고 할 수 있다. 이것을 비지도학습이라고 한다. 오토인코더를 간단하게 그림으로 표현하면 다음과 같다.

위와 같이 데이터를 압축하는 과정 Encode로 압축된 데이터를 생성하고 해당 압축 데이터를 다시 Decode 하여 압축된 정보를 해석도 하는 구조이다. 압축된 정보를 다시 해석할 때 결함 데이터가 생길 수 있다. 즉, 학습 후 추상적인 압축 이미지를 보고 새로운 원본 이미지를 생각해 낼때 결함이 발생할 수 있는데 이 결함에 가상의 데이터를 삽입하여 사용할 수 있다.
이 밖에도 정보를 압축하고 복원하는 구조로 Convolutional layer를 통한 오토인코더 방법인 Convolutional autoencoder 방식과 베이지안적 사고를 바탕으로 신경망을 최적화 시키는 Variational autoencoder등이 제안되었다.
딥러닝, RNN, CNN 구현을 위한 라이브러리는 텐서플로우에서 제공하니 참고
TensorFlow
모두를 위한 엔드 투 엔드 오픈소스 머신러닝 플랫폼입니다. 도구, 라이브러리, 커뮤니티 리소스로 구성된 TensorFlow의 유연한 환경입니다.
www.tensorflow.org
본 포스팅은 딥러닝(논문 저자 : 이승철, 정해동, 박승태, 김수현)을 참고함.